In out previous article, we have discussed about the classification of mechanical energy and it’s first type i.e. Kinetic energy. Now we are going to discuss about the second type of Mechanical energy which is Potential energy.
What is potential energy?
Potential energy of a body is defined as the energy possessed by it by virtue of its position or configuration. Potential energy is measured by the amount of work that is available when the body returns from its present position or configuration to some standard position or configuration, usually called the zero position or configuration.
Examples of Potential Energy
- Let’s understand it with example. Suppose a crane picks up a heavy block from ground to a certain height. The work done by the crane while lifting the block is stored in the block, in its new elevated position as potential energy. Now if the block is released from that height and allowed to descend to the ground, it can do work. It can demolish anything it hits or can compress a spring as it lands.
- When a spring watch is wound, work is done. The spring in the watch stores the work as potential energy. As the spring gradually unwinds to its original relaxed position, it moves the balance wheel of the watch. The potential energy stored in the wound-up spring is used to drive the watch.
What is Gravitational Potential Energy?
The particular kind of potential energy of a raised object is called gravitational potential energy.
The zero configuration is usually taken as the surface of the earth, which is also called the reference level.
How to calculate gravitational potential energy?
A body of mass m is raised to a height h above the surface of the earth. The force F acting on the body is its weight which is mass x gravitational acceleration ie. m.g. Now because of application of the force, the body is raised through a height h, which is the displacement of the body.
Hence the work done = m.g.h

This work is stored up as the potential energy of the body and can be regained by dropping the body back to the ground. Hence, potential energy = m.g.h (in absolute units)
[Please note that the above equation is deduced assuming h is small compared to the radius of the earth so that g may be taken as constant over the distance h]
What will be the potential energy if a body is raised along a slope instead of lifting upright?
Now, let us imagine the scenario when the same body of mass m is lifted along a frictionless inclined plane to a height h. As the body of mass m is pulled upwards along the plane, work must be done against the downward component of its weight mg along the plane viz mg sin θ, while the other component mg cos θ, being normal to the direction of displacement, does not contribute to the total work done.
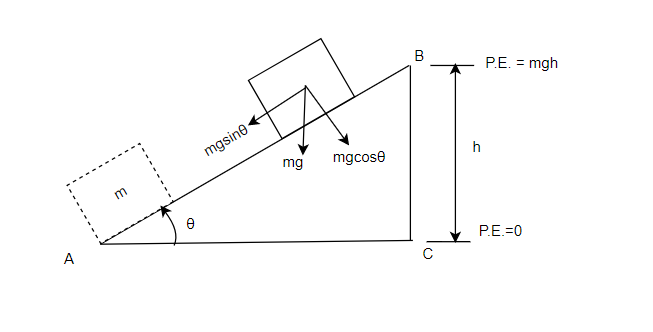
If the body is raised to the point B which is at a height BC = h above the ground,
the total work done = force x displacement
= mg sin θ x AB = mg x AB sin θ = mg x BC = mgh
This proves that the gravitational potential energy equation mgh is valid even if the body is not raised straight upwards to the height h but carried there by any other path.
Gravitational potential must always be specified with respect to some reference level. The expression, mgh, for gravitational potential energy, implies that its value is zero when h=0 that is when the body is at the reference level. The floor of the room or top of table can be considered as reference point.
Can potential energy of a body be negative?
Potential energy of a body can be negative. Let’s consider the scenario that the body of mass m, is located at any point above the reference level. The body has positive potential energy. Now if the same body is taken below the reference level, it will have negative potential energy.
Considering position B as the reference plane, when the body is left on this plane, it has zero potential energy (P.E. =0). On lifting the mass m from B to C, some work is done. On returning from C to B, the body releases energy. Similarly, if it moves from B to A, the body releases energy further.
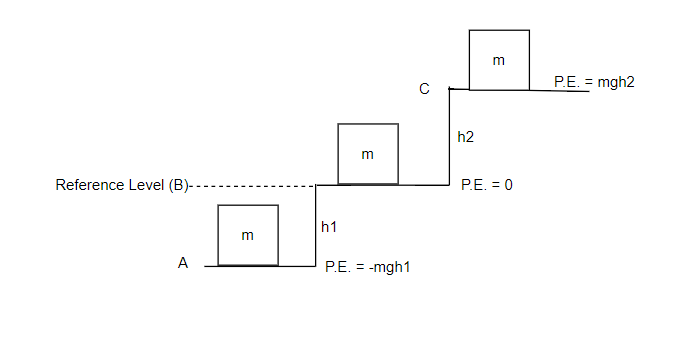
So, the body will possess smaller amount of energy at A compared to B. As the potential energy at B is zero, so the potential energy at point A is negative. On raising it again to B, work must be done to supply the necessary energy. This proves that potential energy can be negative when the object is below the reference level. Another example of negative potential energy is when the earth’s surface is considered as reference level and an object is taken to a mine. As object goes below the earth’s surface which is reference point, the potential energy goes below zero and becomes negative.

1 thought on “Potential Energy – definition and derivation”